Utente:Grasso Luigi/sandbox4/Reticolo dei sottogruppi

In mathematics, the lattice of subgroups of a group ${\displaystyle G}$ is the lattice whose elements are the subgroups of ${\displaystyle G}$, with the partial order relation being set inclusion. In this lattice, the join of two subgroups is the subgroup generated by their union, and the meet of two subgroups is their intersection.

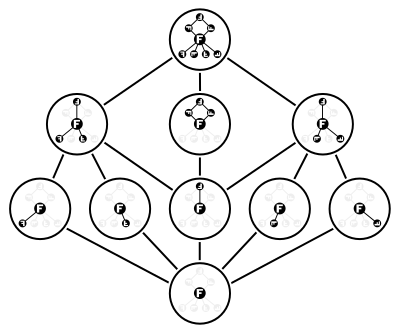
The dihedral group Dih₄ has ten subgroups, counting itself and the trivial subgroup. Five of the eight group elements generate subgroups of order two, and the other two non-identity elements both generate the same cyclic subgroup of order four. In addition, there are two subgroups of the form Z₂ × Z₂, generated by pairs of order-two elements. The lattice formed by these ten subgroups is shown in the illustration.

This example also shows that the lattice of all subgroups of a group is not a modular lattice in general. Indeed, this particular lattice contains the forbidden "pentagon" N₅ as a sublattice.

For any A, B, and C subgroups of a group with A ≤ C (A subgroup of C) then AB ∩ C = A(B ∩ C); the multiplication here is the product of subgroups. This property has been called the modular property of groups Template:Harv or (Dedekind's) modular law (Robinson, Cohn). Since for two normal subgroups the product is actually the smallest subgroup containing the two, the normal subgroups form a modular lattice.

The Lattice theorem establishes a Galois connection between the lattice of subgroups of a group and that of its quotients.

The Zassenhaus lemma gives an isomorphism between certain combinations of quotients and products in the lattice of subgroups.

In general, there is no restriction on the shape of the lattice of subgroups, in the sense that every lattice is isomorphic to a sublattice of the subgroup lattice of some group. Furthermore, every finite lattice is isomorphic to a sublattice of the subgroup lattice of some finite group Template:Harv.

Subgroups with certain properties form lattices, but other properties do not.

• Normal subgroups always form a modular lattice. In fact, the essential property that guarantees that the lattice is modular is that subgroups commute with each other, i.e. that they are quasinormal subgroups.
• Nilpotent normal subgroups form a lattice, which is (part of) the content of Fitting's theorem.
• In general, for any Fitting class F, both the subnormal F-subgroups and the normal F-subgroups form lattices. This includes the above with F the class of nilpotent groups, as well as other examples such as F the class of solvable groups. A class of groups is called a Fitting class if it is closed under isomorphism, subnormal subgroups, and products of subnormal subgroups.
• Central subgroups form a lattice.

However, neither finite subgroups nor torsion subgroups form a lattice: for instance, the free product ${\displaystyle \mathbf {Z} /2\mathbf {Z} *\mathbf {Z} /2\mathbf {Z} }$ is generated by two torsion elements, but is infinite and contains elements of infinite order.

The fact that normal subgroups form a modular lattice is a particular case of a more general result, namely that in any Maltsev variety (of which groups are an example), the lattice of congruences is modular Template:Harv.

Lattice theoretic information about the lattice of subgroups can sometimes be used to infer information about the original group, an idea that goes back to the work of Template:Harvs. For instance, as Ore proved, a group is locally cyclic if and only if its lattice of subgroups is distributive. If additionally the lattice satisfies the ascending chain condition, then the group is cyclic.

The groups whose lattice of subgroups is a complemented lattice are called complemented groups Template:Harv, and the groups whose lattice of subgroups are modular lattices are called Iwasawa groups or modular groups Template:Harv. Lattice-theoretic characterizations of this type also exist for solvable groups and perfect groups Template:Harv.

• M. Aschbacher, Finite Group Theory, Cambridge University Press, 2000, p. 6, ISBN 978-0-521-78675-1.
• Reinhold Baer, The significance of the system of subgroups for the structure of the group, in American Journal of Mathematics, vol. 61, n. 1, The Johns Hopkins University Press, 1939, pp. 1–44, DOI:10.2307/2371383.
• Paul Moritz Cohn, Classic algebra, Wiley, 2000, p. 248, ISBN 978-0-471-87731-8.
• Über die endlichen Gruppen und die Verbände ihrer Untergruppen, in J. Fac. Sci. Imp. Univ. Tokyo. Sect. I., vol. 4, 1941, pp. 171–199.
• The Shape of Congruence Lattices, American Mathematical Soc., 2013, p. 3, ISBN 978-0-8218-8323-5.
• Øystein Ore, Structures and group theory. I, in Duke Mathematical Journal, vol. 3, n. 2, 1937, pp. 149–174, DOI:10.1215/S0012-7094-37-00311-9.
• Øystein Ore, Structures and group theory. II, in Duke Mathematical Journal, vol. 4, n. 2, 1938, pp. 247–269, DOI:10.1215/S0012-7094-38-00419-3.
• Derek Robinson, A Course in the Theory of Groups, Springer Science & Business Media, 1996, p. 15, ISBN 978-0-387-94461-6.
• Ada Rottlaender, Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen, in Mathematische Zeitschrift, vol. 28, n. 1, 1928, pp. 641–653, DOI:10.1007/BF01181188.
• Roland Schmidt, Subgroup Lattices of Groups, Walter de Gruyter, 1994, ISBN 978-3-11-011213-9. Review by Ralph Freese in Bull. AMS 33 (4): 487–492.
• Michio Suzuki, On the lattice of subgroups of finite groups, in Transactions of the American Mathematical Society, vol. 70, n. 2, American Mathematical Society, 1951, pp. 345–371, DOI:10.2307/1990375.
• Michio Suzuki, Structure of a Group and the Structure of its Lattice of Subgroups, Berlin, Springer Verlag, 1956.
• B. V. Yakovlev, Conditions under which a lattice is isomorphic to a lattice of subgroups of a group, in Algebra and Logic, vol. 13, n. 6, 1974, pp. 400–412, DOI:10.1007/BF01462952.
• Caratterizzazione dei gruppi risolubili d'ordine finito complementati, in Rendiconti del Seminario Matematico della Università di Padova, vol. 22, 1953, pp. 113–122.

• PlanetMath entry on lattice of subgroups
• Example: Lattice of subgroups of the symmetric group S4